Because doubters appear here, i have decided to make things clear once and forever.
The root of inspiration is methodology used by RedHotPawn game mods, reintroduced by Steve Collyer to the public in 2009 in the infamous Ouachita's case at Chess.com.
Original method uses any modern chess engine (e.g. Fritz10, Fritz11, Rybka etc) running under fixed time condition, usually 30 seconds, showing top choices. Manually feasible with stopwatch in almost any UCI. RHP game mods used this to support their suspicion of engine smell with something more robust than just some uncertain feelings. They analyzed many top OTB and especially pre-computer era correspondence games to obtain values for honest play. After testing many games with many engines, they made an estimation of top amateur human correspondence honest play as top1 max. 60%, top2 max. 75% and top3 max. 85%. To avoid false positives, they added +5% and declared that everyone above 65%, 80% and/or 90% on reasonable big sample (at least 400 moves, recommended 20 games with 20 non-book moves each against solid opposition) is blatant cheater. They created program called Batch Analyzer to perform such analysis automatically.
Well inspired, i downloaded another analyzer here, paid for full version (weird, isn't it?) and went my own way. The main difference is that i decided to use fixed depth of engine Firebird instead of fixed time.
I analyzed XI. WCCh (1983 - 1988, winner Friedrich Baumbach, 15 players) to obtain benchmarks. I should mention, the main parameter to be watched is Top3.
Obtained results:
Top3 ... 3809 of 4587 moves => 83.04 %
Theoretical calculated binomial standard deviation of the whole sample ... 0.55 %
Calculated residual individual standard deviation by players ... 0.92 % (pythagorean difference between individual total and individual binomial standard deviation)
Total standard deviation of suspect is pythagorean sum of three parts:
constant 0.55 % (binomial benchmark)
constant 0.92 % (residual, considering minor inadequacy of binomial model and differences in playing style)
player's sample binomial (inverse-proportional to square-root of number of analyzed moves)
Forced and obvious moves are used in both, benchmark sample and analyzed sample of suspect. There is no reason to assume that in online chess are these moves more frequent than in ancient correspondence and can create significant bias. Playing styles prefering more forced moves and inadequacy of binomial model are considered in the pythagorean sum of deviations (see above).
The reasonable cut-off line is +2.5 total standard deviations, which is about 99th percentile in the case the player in question is pre-computer correspondence chess grandmaster (most of them obviously aren't and even Docx and Dembo should be considered as much weaker correspondence players than XI. ICCF finalists).
The minimum total standard deviation is 1.07 % for sample with infinite number of moves.
Thus players with Top3 under 85.72 % are considered as undetectable with this method. :o)
The first possible source of bias is opening theory checked & created with computer assistance nowadays. Non-book moves are cut, but so are first 3 nonbook moves to avoid bias from pre-game preparation with computer and private knowledge of a player in his/her pet opening, checked by computer.
Another possible source of bias is the fact that online players today play very often until checkmated, while ancient correspondence players always resigned, because postal cards were somewhat expensive, especially in international competitions. Thus the game is considered determined, when the evaluation exceeds 3 pawn units and rest is cut. However even after these two cuts, there must remain at least 17 moves, shorter games are either show-draws or low quality opposition.
Edit 29th April: Graph of benchmark data, 15 players Top3 statistics. Note: number of moves they played is signicantly lower than number of moves played by suspects, thus the variation is higher.
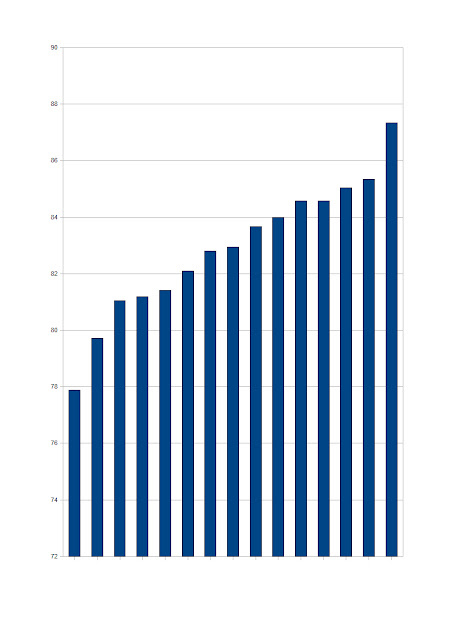
Question: Is the Top3 benchmark material from XI. WCCh symmetrically distributed around the mean value?
ReplyDeleteOne question regarding the benchmark: how come you analyse a group of players (all participants in the tournament) and not individual players? Baumbach for example should definitely have enough games available against top class opposition.
ReplyDeleteAnother question: What happens if the evaluation increases above 3 pawn units but at a later stage drops below this? There are positions which the computer evaluates well above 3.0 which are theoretically drawn.
ReplyDeleteRegarding that the analysed payers are not as strong as the people in the benchmark, wasn't there a real-world CC GM (from early 90s which on that level definitely is pre-computer) that was driven away from chess.com by yourself and others like you?
ReplyDelete1) Yes, at least graphically
ReplyDelete2) I have analyzed top3 of individual players in this tournament and derived a residual standard deviation from it.
3) It never happens in cheated games. I consider the game won once it exceeds 3 pawn units, if the final result is the same. This is to avoid bias from benchmark data, where games with such advantage were very rarely played.
4) Jan Ohlin aka snrf? He decided to leave himself. If i remember well, he was treated politely by everyone. He wrote several posts, where he explained his views, especially the one that correspondence/online chess with computers banned is scam and computers should be allowed everywhere. This created quite heated discussion, btw this is common attempt of cheaters, to argue for ICCF and defend themselves this way. So this aroused my curiosity and i analyzed his games. Unfortunately, there weren't enough quality games to run top3 as described above, so i used another method and come to conclusion he is very likely cheater too. But i can't reveal him as cheater, unless i make more serious tests in the future.
Earlier question: Is the Top3 benchmark material from XI. WCCh symmetrically distributed around the mean value?
ReplyDeleteAnswer by Polar_Bear: 1) Yes, at least graphically
Reply: I doubt that this is true; please, provide data! I suspect that the distribution will be asymmetric with a long "tail" into the positive region (and a much shorter wing in the negative direction), and that your analysis is therefore entirely flawed.
To anonymous poster: With serious discussion, please contact me via e-mail.
ReplyDeleteThe plot at the level of the individual players' mean Top3 percentage is clearly too crude to reveal the distribution of the benchmark data. The same plot at the level of the individual matches is required in order to decide.
ReplyDeleteIt seems that the Blogger has applied the theory of binomial distribution on the data. Such a model requires that the probability of a hit (convergence with computer move) is the same on every trial (move). Moreover, treatment by this theory requires the trials (moves) to be independent of one another. I doubt that either requirement is fulfilled here.
This is an important comment. Unless Polar_Bear can prove that his methodology is mathematically adequate, there is only one conclusion: His entire analysis is worthless and he should post an apology to the chess community.
ReplyDeleteTo Polar_Bear (in reply to: With serious discussion, please contact me via e-mail)
ReplyDeleteWhy not have the serious discussion for everyone to see? You've got something to hide?
An e-mail contact would be private and could even lead to another erroneous accusation of cheating on this blog :) so, thank you, no!
I have never made any statement that binomial distribution is an ideal model, however this fact has been taken into account with additional part of standard deviation. You should read more carefully.
ReplyDeleteBenchmark data aren't ideally symetrical, real data never are, but the skewness is small and negative: -0.27, thus the tiny "tail" is in negative region. And kurtosis is positive, thus the application of the chosen interval is even more strict than with normal distribution. These facts very likely even reduce the risk of false positivity.
I kinda dislike anonymous trolls. My patience is going to be exhausted.
ReplyDeleteAs mere anonym you aren't in position to make such demands and conclusions. Bye.
The important simple question is whether the binomial model of statistical analysis is at all applicable in this case. The model requires that the probability that a suspect player makes a computer-predicted move (one of the computer's three best) is the same at each move in a game. It also requires that each move in the game is independent of other moves. The first is quite unlikely to be true especially for honest players. The second requirement is highly unlikely due to the nature of the game of chess, and of course just about impossible at a high level of the game.
ReplyDeleteObviously, two key textbook requirements for a binomial model such as the one on this blog are not met. This means that the entire analysis is seriously flawed.
In reply to Polar_Bear: No demands are made with this, just a statement of absolute textbook fact that anyone who reads this can verify him/herself. The fact is not changed and the matter no different by my anonymity.
I also don't think this post can be classified as trolling, except when the reader does not like to look at facts. If the Blogger wants to have serious scientific back-up for his crusade against cheaters, he should use scientifically impeccable methods.
The answer to the main question is:
ReplyDeleteYes, the classic binomial distribution is applicable here under certain conditions, which are: reasonably big sample and additional part of standard deviation.
Unfortunately, Poisson binomial distribution, which would fit better and would allow to run smaller samples, is not applicable here, unless you create some function (depending on evaluation and number of reasonable moves) to estimate variable probability of individual hints. And i would bet you either get similar results on big samples or you take in an unwanted unknown bias with untested function on smaller ones. In any event, it would cost 20x more work, the benefit would be small and forum anonyms still would dispute it.
This comment has been removed by a blog administrator.
ReplyDeleteIf you think my model is flawed, replicate my analysis, create data and prove it. And don't forget to prove that my conclusions about cheaters are wrong.
ReplyDeleteI don't need to prove that it is flawed, because your treatment violates two central requirements of the theory. That is textbook stuff!
ReplyDeleteI have said nothing about your conclusions about cheaters, only noted that you cannot base ANY conclusions on a model in which two basic postulates of the underlying theory are violated.
Hahaha, so you come to the conclusion, that Poisson binomial distribution would be also flawed. Really, great deduction! Just more unknown parameters.
ReplyDeleteWell, more seriously. We talk about high numbers of moves & games and the overall probability. Your objection about self-dependence of moves would make sense in the small sample of games (let's say up to 5), where one random exceptional game would create bias of the whole sample. And the probability of such bias IS ALREADY CALCULATED AND TAKEN INTO ACCOUNT in the additional part of standard error.
So, questions answered, objections refuted and doubts cleared.
Violating two of the basic requirements for this theory is not counteracted by large samples. This is chess and not flipping a coin, and does not look more like the latter by increasing sample size.
ReplyDeleteYes, i know it and I have taken it into account. Read first before you post.
ReplyDeleteThis comment has been removed by a blog administrator.
ReplyDeleteThe discussions with fat-heads, who are unable to understand that i am aware of the complexity of the problem and take it into account with additional uncertainity, are really boring.
ReplyDeleteConsequently, this fat-head will bore you no longer. The point has been made.
ReplyDeleteAnother fat-head is asking on the basis of the statement: "Non-book moves (meaning book moves [anonymous'comment]!) are cut, but so are first 3 nonbook moves to avoid bias from pre-game preparation with computer and private knowledge of a player in his/her pet opening, checked by computer"
ReplyDeleteQuestion: Is cutting the first 3 nonbook moves also done for the benchmark material?
No. Theory developed quite a lot since then.
ReplyDeleteIn you graph, I suspect that the bar to the right is Baumbach. If this is indeed the case, wouldn't he based on this be above your 2.5 % standard deviation allowance and based on this be called a cheater according to your definition?
ReplyDeleteYou claim that the number of moves is lower, but if you were to complete it with baumbachs games from another tournament?
If this is the case doesnt it contradict the bold statement:
"Top3 figures of the members above were never observed in the games from pre-computer CC era"?
The highest bar in the right is Nesis, he came 2nd because of worse S.B. (he lost his game to Baumbach). I was considering to remove him, because there were first computers (Psion, Sargon, Mephisto) and i suspect him to use one. I decided to keep him in after some hesitation.
ReplyDeleteSo whenever, even in the reference material, the Top3 score exceeds what Zeman has decided is "honest play", he declares suspicion of cheating. Now we are talking about a very highly appreciated world class player and coach, Gennady Nesis.
ReplyDeleteIt can't be cheating since ICCF permits use of computers, and besides any engines available in the 80s were completely useless to a serious CC player. Interesting though that this made Zeman consider to remove Nesis from the benchmark. Nesis numbers indicated computer assistance...(even if that happened to be impossible because of the timing) thus he must be using a computer..but wait a minute, this reasoning is going around in circles.
ReplyDeleteAncient computers already existed. AFAIK they were sometimes used by computer fans at lower levels.
ReplyDeleteA player with results identical to Nesis's would be only 1.97 standard deviations above - not mentioned here as cheater (but monitored further however).
ICCF local rules do not prohibit computers. I know that. It has however zero importance for Chess.com and this blog.
Just a brief note no chess engines in the 80s: They were weak, the publicly available rarely above OTB playing strength 1800. Nesis lived in the former Soviet Union, very unlikely to have access to a PC. If you ran a match-up with these engines on relevant hardware from the 80 vs a modern PC with a modern engine (say Rybka, Fritz or Fire) you would see a radical difference.
ReplyDeleteThis use of "Ancient computers" in the discussion is a smoke-screen and nothing else. If you seriously believe it affects the benchmark, why did you pick this particular WCCC? there are plenty of older ones.
Oh yes, it is a little mystery. I thought the same way and thus decided to keep Nesis in. It has made main value and standard deviation both little higher. It is a good thing for anonymous sceptics, isn't it?
ReplyDeleteYou should not say "main" when you (probably) mean "mean"
ReplyDeleteWhen someone is honestly 55% right, that's very good and there's no use wrangling. And if someone is 60% right, it's wonderful, it's great luck, and let him thank God. But what's to be said about 75% right? Whoever says he's 100% right is a fanatic, a thug, and the worst kind of rascal." An Old Jew of Galicia (From The Captive Mind by Czeslaw Milosz)
ReplyDeletePolar_Bear's methodology is fair in the sense that it is openly explained, thus transparent and open to scrutiny and criticism. Despite weaknesses in the statistical methodology, the method is also fair in the sense that it aims at computing the probability of someone using chess programs to aid their game. By complete contrast, chess.com (D.Pruess) claims that they KNOW for CERTAIN before banning someone for cheating. That is unscientific nonsense and blatant cheating by itself. It is actually scary that at the same time as chess.com bans a player (Fezzik) whose Top 3 <90% and barely over 3 standard errors (P_B methodology) they do not ban players among the 15 highest ranked with Top3 a lot over 90% and with standard errors way over 5!
ReplyDeletePlayers on chess.com frequently get banned for discussing known flaws in this methodology and suggesting (in a constructive way) possible improvements.
ReplyDeleteWhile I understand the secrecy involved in necessary to prevent cheaters from changing tactics...if you have nothing to hide you don't ban people for having a different opinion, especially if they're more knowledgeable than most about the process and chess in general. No different from Nazis burning books.
you aren't chess.com staff... wonder why you bother spending much time just to catch cheaters of a site you don't even develop/maintain. too many cheaters over there... but hey this isn't anyone's nation.
ReplyDeleteWhat bothers me most about your criteria is that as long as a cheater makes sure the game ends, in under a certain amount moves every time or they intentionally play the worst moves that still give an advantage or keep the game roughly equally, waiting for a mistake, they seem immune to your system's prerequisites.
ReplyDeleteI am aware of that. So when one's side advantage goes beyond certain level, rest of the game is discarded. This little feature allows to catch most of these sly-foxes easily especially when they play other cheats. However when they play weak honest amateurs, the game rarely contains useful data to prove anything.
ReplyDeleteSome contribution about Nesis.
ReplyDeleteComputers and programs in his time were very awkward. Any sane CM could beat them with proper attitude.
The thing is that Nesis had some strong friends and chess students, whose help he used for the analysis - among them, for example, Alexander Khalifman, so it was really a miracle that he did not win that championship. The same can be said about Estrin - he constantly asked top Soviet GMs to help him in the analysis.